Metapopulations
BIO605
Population ecology
Population ecology
What do population ecologists study?
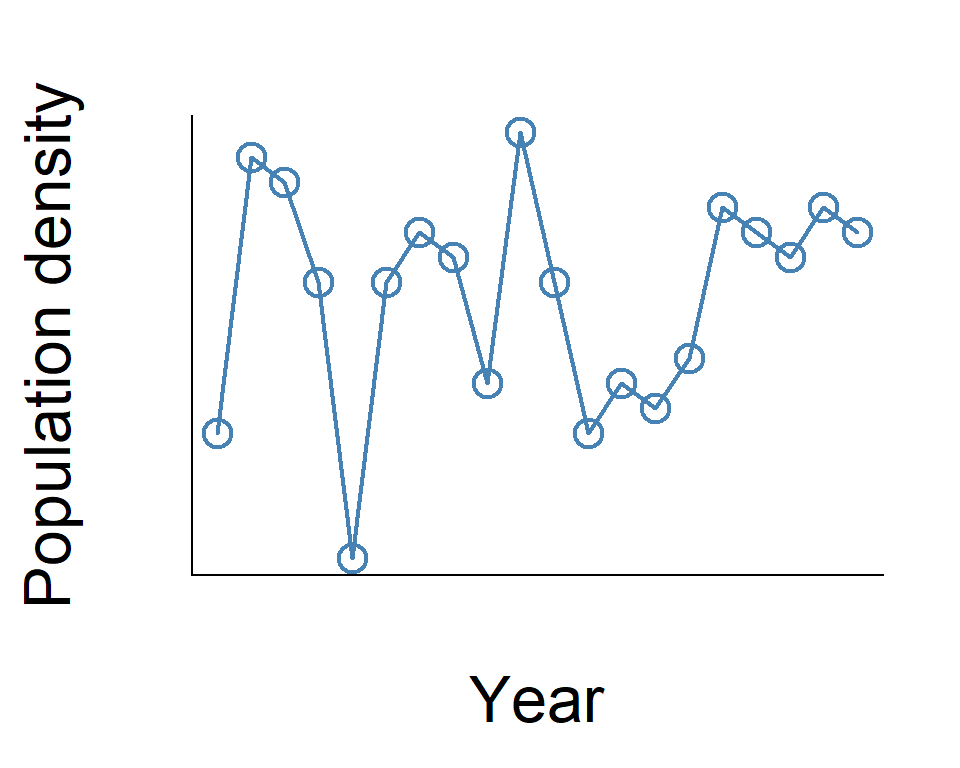
Population dynamics — how population size/density changes over time in a single habitat
Distributions — how populations are distributed over space
Landscape-level dynamics — how populations are maintained at the landscape level (metapopulation)
Examples
Population dynamics
birth & death
(immigration, emigration)
Spatial distribution
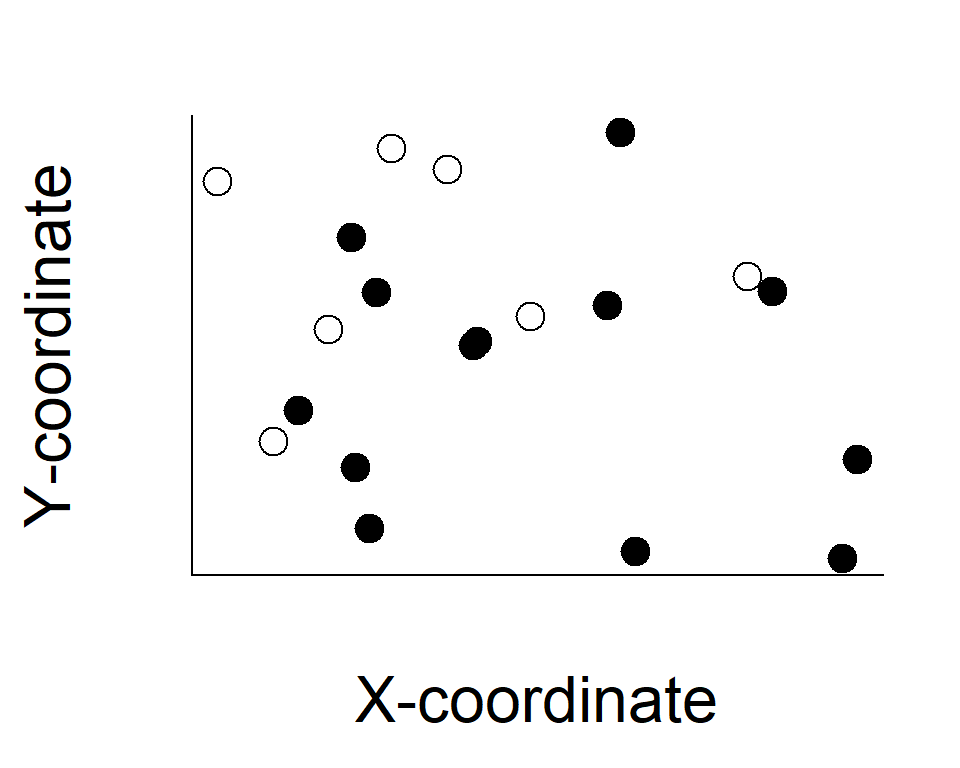
local environments, dispersal
Classical metapopulation
What is a metapopulation?
Population of populations
- Populations are connected by dispersal
- Does this make difference?
Recall: local population
Local population dynamics with no dispersal is driven by birth \(b\) and death \(d\) processes
\[ \frac{dN}{dt} = (b - d)N \]
Once the population goes extinct, no chance to re-establish a new population
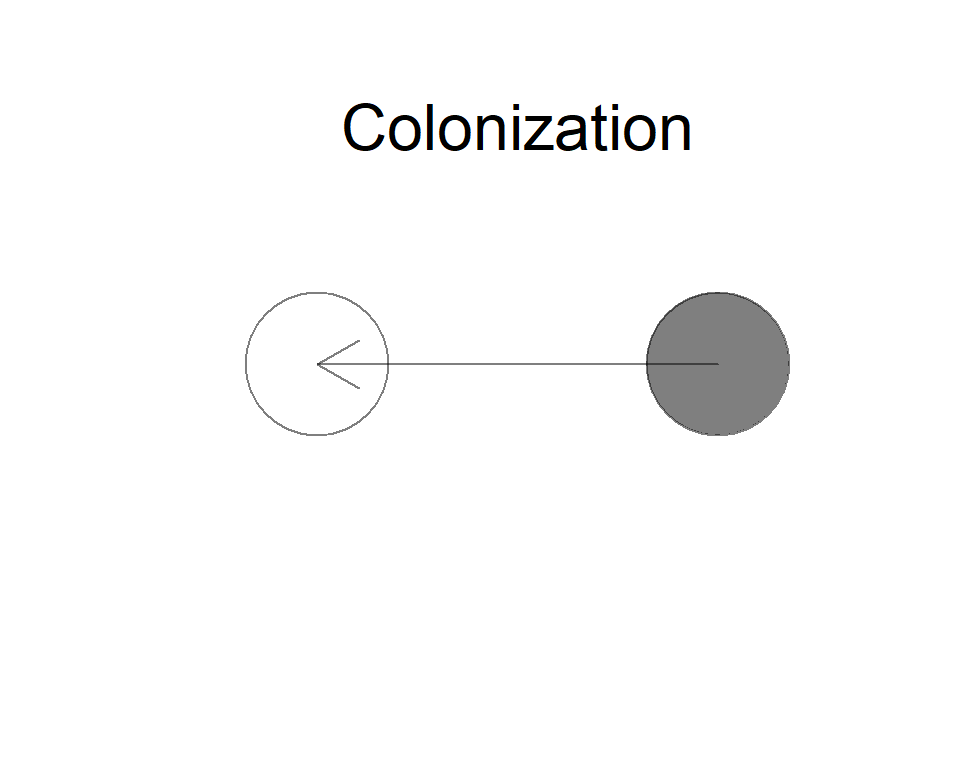
Immigration
Immigration can lead to a colonization into a new habitat
Metapopulation theory
Classical metapopulation theory focuses on dynamics at a landscape level
- Local population dynamics are not explicitly modeled
- either
occupiedorunoccupied - no information on population size
- either
- Metapopulation persistence is the primary interest
- how patch occupancy changes over time
- key: colonization \(m\)* and extinction rates \(e\)*
*Parameter notations may differ among studies
Levins metapopulation model
The Levins Metapopulation Model:
\[ \frac{dp}{dt} = mp(1-p) - ep \]
- \(p\): proportion of patches occupied
- \(m\): colonization rate (per patch)
- \(e\): extinction rate (per patch)
Levins (1969) Some demographic and genetic consequences of environmental heterogeneity for biological control. Bulletin of the Entomological Society of America. 15: 237-240
Colonization
The Levins Metapopulation Model:
\[ \frac{dp}{dt} = mp(1-p) - ep \]
The term \(mp(1-p)\) determines the rate of increase in occupancy
- immigrants come from occupied patches (\(p\))
- colonization occurs only at unoccupied patches
- multiply \(m\) to express random colonization
Extinction
The Levins Metapopulation Model:
\[ \frac{dp}{dt} = mp(1-p) - ep \]
The term \(ep\) determines the rate of decrease in occupancy
- extinction occurs only at occupied patches (\(p\))
- multiply \(e\) to express random extinction
R exercise: colonization
Draw how colonization rate changes over \(p\)
Create \(p\) and \(m\) (set 1.0 for an example)
R exercise: colonization
Draw how colonization rate changes over \(p\)
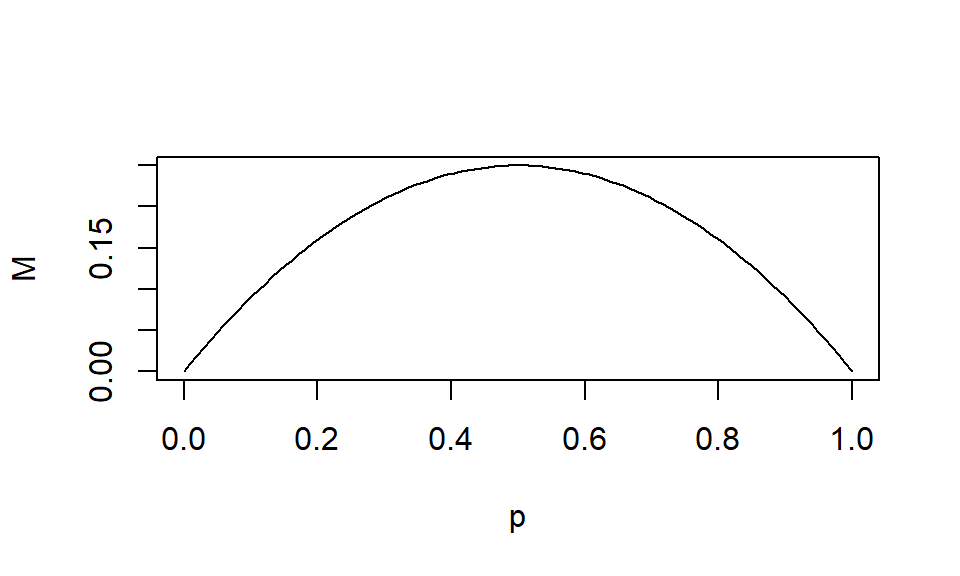
Plot the relationship b/w \(p\) and \(mp(1-p)\)
R exercise: colonization
Draw how colonization rate changes over \(p\)
Plot the relationship b/w \(p\) and \(mp(1-p)\)
R exercise: extinction
Draw how extinction rate changes over \(p\)
Create \(e\) (set 0.2 for an example)
R exercise: extinction
Draw how extinction rate changes over \(p\)
Plot the relationship b/w \(p\) and \(ep\)
R exercise: extinction
Draw how extinction rate changes over \(p\)
Plot the relationship b/w \(p\) and \(ep\)
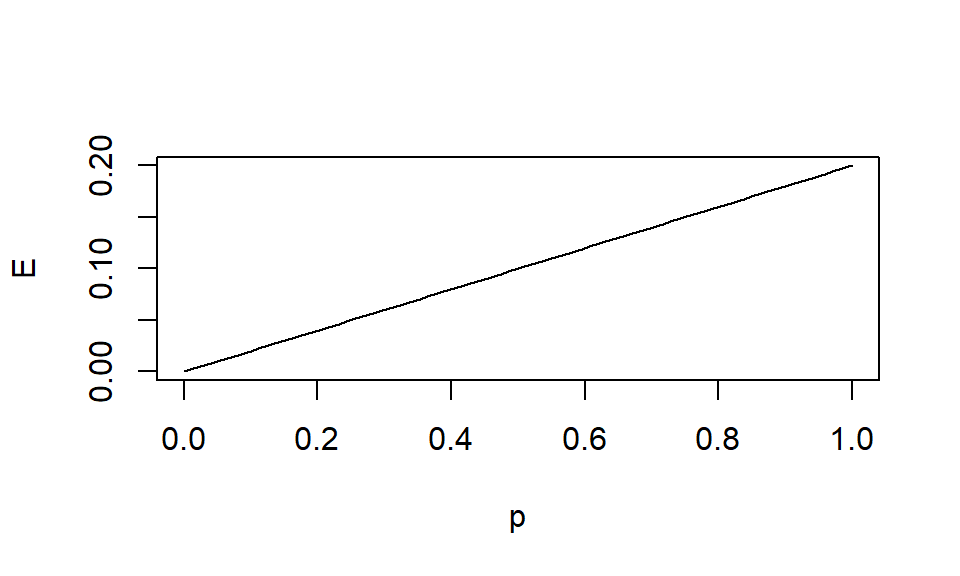
R exercise: m & e
Draw how colonization & extinction rates change over \(p\)
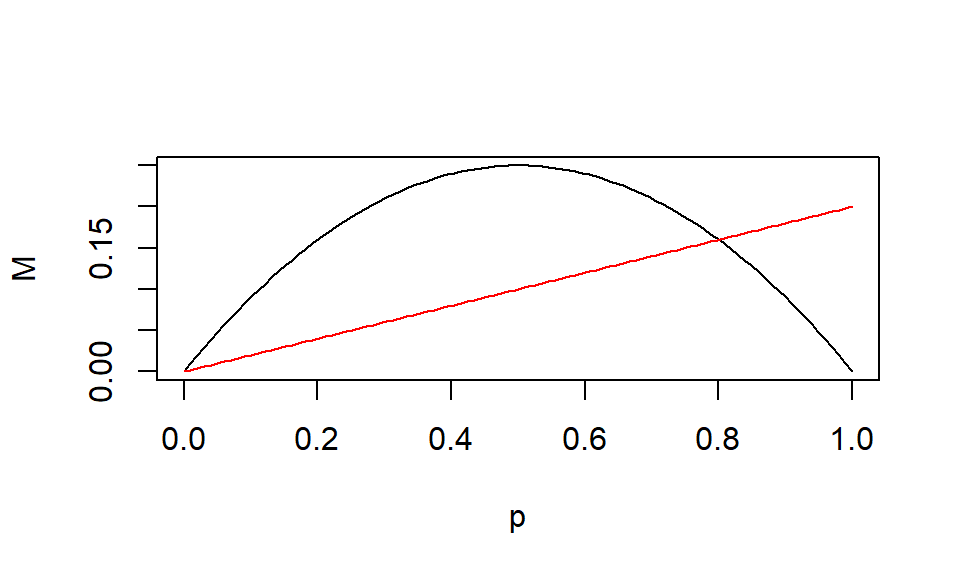
Equilibrium occupancy

- With \(p\) below the intersection, occupancy ___
- With \(p\) above the intersection, occupancy ___
Equilibrium occupancy
\[ \frac{dp}{dt} = mp(1-p) - ep \]

Equilibrium occupancy
How to get equilibrium occupancy?
Equilibrium occupancy
Solve the following eq. about \(p\)
\[ \begin{align} \frac{dp}{dt} &= cp(1-p) - ep = 0\\ p^* &= ...\\ \end{align} \]
Equilibrium occupancy
Solve the following eq. about \(p\)
\[ p^* = 1 - \frac{e}{m} \]
Condition for persistence
For a metapopulation to persist, \(p^*\) > 0
\[ p^* = 1 - \frac{e}{m} > 0 \]
Condition for persistence
For a metapopulation to persist, \(p^*\) must exceed zero, meaning
\[ m > e \]
Colonization rate \(m\) must exceed extinction rate \(e\)
Link to logistic model
The Levins Metapopulation Model:
\[ \frac{dp}{dt} = mp(1-p) - ep \]
can be transformed to:
\[ \frac{dp}{dt} = (m-e)p(1-\frac{p}{1-\frac{e}{m}}) \]
Link to logistic model
Express differently
\[ \frac{dp}{dt} = (m-e)p(1-\frac{p}{1-\frac{e}{m}}) \]
Let (1) \(p = N\), (2) \(m-e = r\), and (3) \(1-\frac{e}{m} = K\)
\[ \frac{dN}{dt} = rN(1-\frac{N}{K}) \]
Thus, the Levins metapopulation model can be seen as a logistic model at a different spatial scale
NOTE: not identical as \(0 \le p \le 1\)
Assumptions
Classical metapopulation assumes
- No variation in population size
- Immigration from within-metapopulation sources
- Random colonization & extinction
- Dispersal do NOT affect population dynamics
Mainland-island metapopulation model
One of the assumptions in the Levins metapopulation model is equal population size
The mainland-island metapopulation model is on the other extreme
Levins vs. mainland-island

Assumptions
- One LARGE population (the mainland) that never goes extinct
- Immigration from the mainland to islands only
- Random extinctions on islands
The formula
The mainland-island metapopulation model:
\[ \frac{dp}{dt} = m(1-p) - ep \]
The Levins metapopulation model:
\[ \frac{dp}{dt} = mp(1-p) - ep \]
R exercise: colonization
Draw how colonization/extinction rate changes over \(p\)
Create \(p\), \(m\) and \(e\)
R exercise: colonization
Draw how colonization/extinction rate changes over \(p\)
Create \(m(1-p)\) and \(ep\)
R exercise: colonization
Plot \(m(1-p)\) and \(ep\)
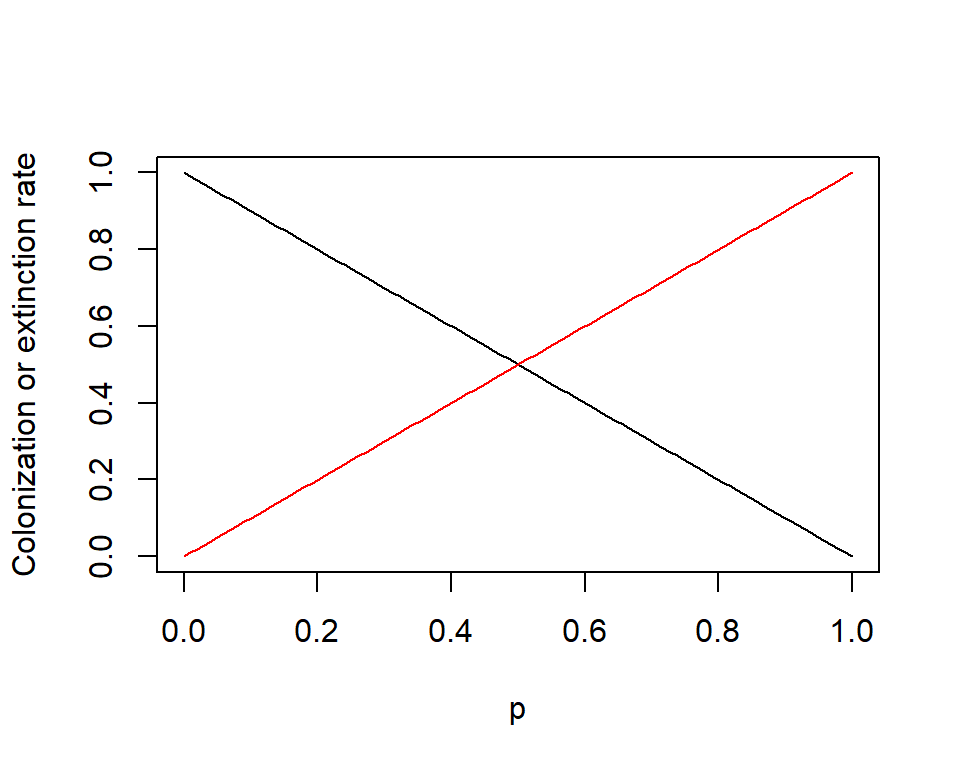
Equilibrium
The mainland-island metapopulation model:
\[ \frac{dp}{dt} = m(1-p) - ep \]
The equilibrium occupancy \(p^*\) is
\[ p^* = ... \]
Equilibrium
\[ p^* = \frac{m}{m+e} \]

Condition for persistence
For a metapopulation to persist, \(p^* > 0\)
\(\frac{m}{m+e} > 0\), i.e., \(m > 0\)
Condition for persistence
When \(m > 0\), there is a persistent supply of immigrants from the mainland
- the metapopulation never goes extinct
- higher extinction rate \(e\) cannot lead to the metapopulation extinction
Field study
More complexity
The metapopulation models are clearly oversimplified
In particular…
- Random extinction
- Random colonization
Assumptions
Random extinction
Population size varies in nature and influences local extinction risk
Random colonization
Organisms have limited dispersal capability
Proxies
Focus on a single habitat patch and think colonization into and extinction of the patch
Proxies
Habitat size
Extinction probability decreases with increasing habitat size

Rationale: habitat size
In a large habitat…
- population size is larger
- more refuge
Proxies
Isolation
Colonization probability decreases with increasing isolation

Rationale: isolation
In a isolated habitat,
- dispersal is more costly & risky
- dispersing individuals are less likely to arrive
Measures of isolation
- distance to the nearest neighbor
- distance weighted measure
Empirical approach
When studying real organisms…
- survey presence/absence of the species \(y_i\) at each habitat
- relate to habitat size and isolation (and other factors)
\[ y_i = f(habitat~size, isolation) \]
Reality
More reality might be needed for empirical studies
- matrix permeability
- wind
- current
- species interactions
Gap
Theory: metapopulation-level occupancy
Empirical: patch-level occupancy
Testing metapopulation theory
Patch-level studies can still provide insights
However, our primary interest is the metapopulation persistence, not persistence of local populations
Approach to studying metapopulations
Metapopulation replicates are needed to study the drivers of metapopulation persistence
or
Scaling up with simulation approaches with parameters estimated with patch-level studies