brnet • mcbrnet

Basic usage

brnet() generates a random branching network with the specified number of patches and the probability of branching. The key arguments are the number of habitat patches (n_patch) and the probability of branching (p_branch), which users must specify. With these parameters, the function generates a branching network through the following steps:

Draw the number of branches in the network. An individual branch is defined as a series of connected patches from one confluence (or outlet) to the next confluence upstream (or upstream terminal). The number of branches in a network $N_{b}$ is drawn from a binomial distribution as $N_{b} \sim Binomial(N,P_{b})$ , where $N$ is the number of patches and $P_b$ is the branching probability.
Draw the number of patches in each branch. The number of patches in branch $q$ , $n_q$ , is drawn from a geometric distribution as $n_{q} \sim Ge(P_b)$ but conditional on $\sum_{q}^{N_{b}} n_q = N$ .
Organize branches into a bifurcating branching network.

The function returns:

adjacency_matrix: adjacency matrix.
distance_matrix: distance matrix. Distance between patches is measured as the number of steps required to reach from the focal patch to the target patch through the network.
df_patch: data frame (dplyr::tibble) containing patch attributes.
- patch_id: patch ID.
- branch_id: branch ID.
- environment: environmental value at each patch (see below for details)
- disturbance: disturbance level (i.e., proportional mortality) at each patch (see below for details)
- n_patch_upstream: the number of upstream contributing patches (including the focal patch itself; akin to the watershed area in river networks).

Quick start

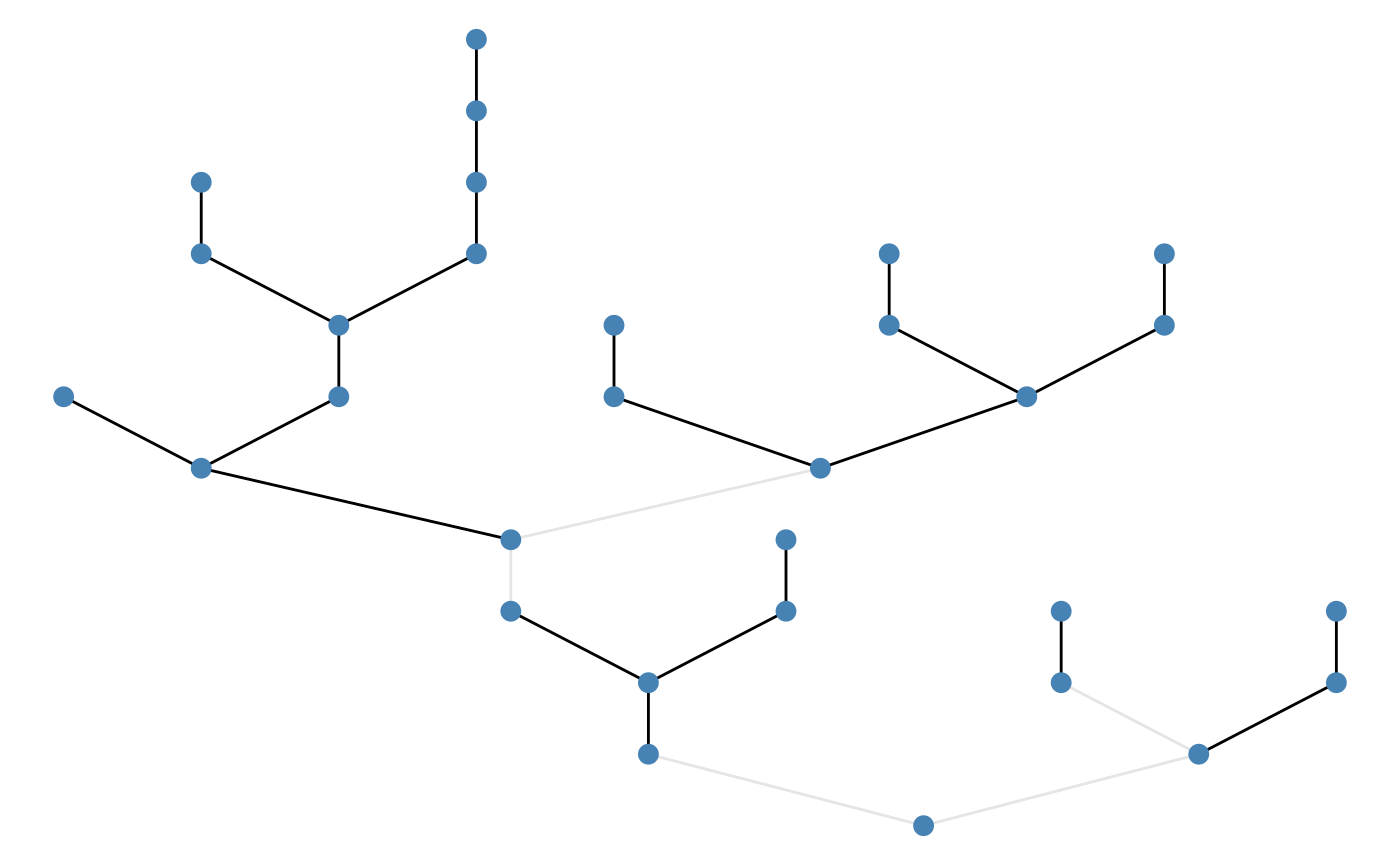
The following script produce a branching network with n_patch = 50 and p_branch = 0.5. By default, brnet visualizes the generated network using functions in R packages igraph and ggraph (plot = FALSE to disable):

net <- brnet(n_patch = 50, p_branch = 0.5)

By default, patches are colored based on environmental values.

To view matrices, type the following script:

# adjacency matrix
# showing 5 patches for example
net$adjacency_matrix[1:5, 1:5]
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    0    0    0    0    0
#> [2,]    0    0    1    0    0
#> [3,]    0    1    0    0    0
#> [4,]    0    0    0    0    1
#> [5,]    0    0    0    1    0

# distance matrix
# showing 5 patches for example
net$distance_matrix[1:5, 1:5]
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    0    4    5    7    8
#> [2,]    4    0    1    7    8
#> [3,]    5    1    0    8    9
#> [4,]    7    7    8    0    1
#> [5,]    8    8    9    1    0

The following script shows patch ID, branch ID, environmental values, disturbance values, and the number of upstream contributing patches for each patch:

net$df_patch
#> # A tibble: 50 × 5
#>    patch_id branch_id environment disturbance n_patch_upstream
#>       <int>     <dbl>       <dbl>       <dbl>            <dbl>
#>  1        1         1      -1.33        0.861               50
#>  2        2        10      -1.13        0.967                6
#>  3        3        10      -1.05        0.970                5
#>  4        4         7      -0.833       0.831               16
#>  5        5         7      -0.665       0.848               15
#>  6        6        13      -0.890       0.712                5
#>  7        7        13      -0.938       0.705                4
#>  8        8        13      -0.967       0.727                3
#>  9        9        13      -1.06        0.738                2
#> 10       10        13      -1.18        0.728                1
#> # ℹ 40 more rows

Customize: visualization

Arguments: patch_label, patch_size

Users may add patch labels using the argument patch_label:

# patch ID
brnet(n_patch = 50,
      p_branch = 0.5) %>% 
  ggbrnet(patch_label = "patch")

# branch ID
brnet(n_patch = 50,
      p_branch = 0.5) %>% 
  ggbrnet(patch_label = "branch")

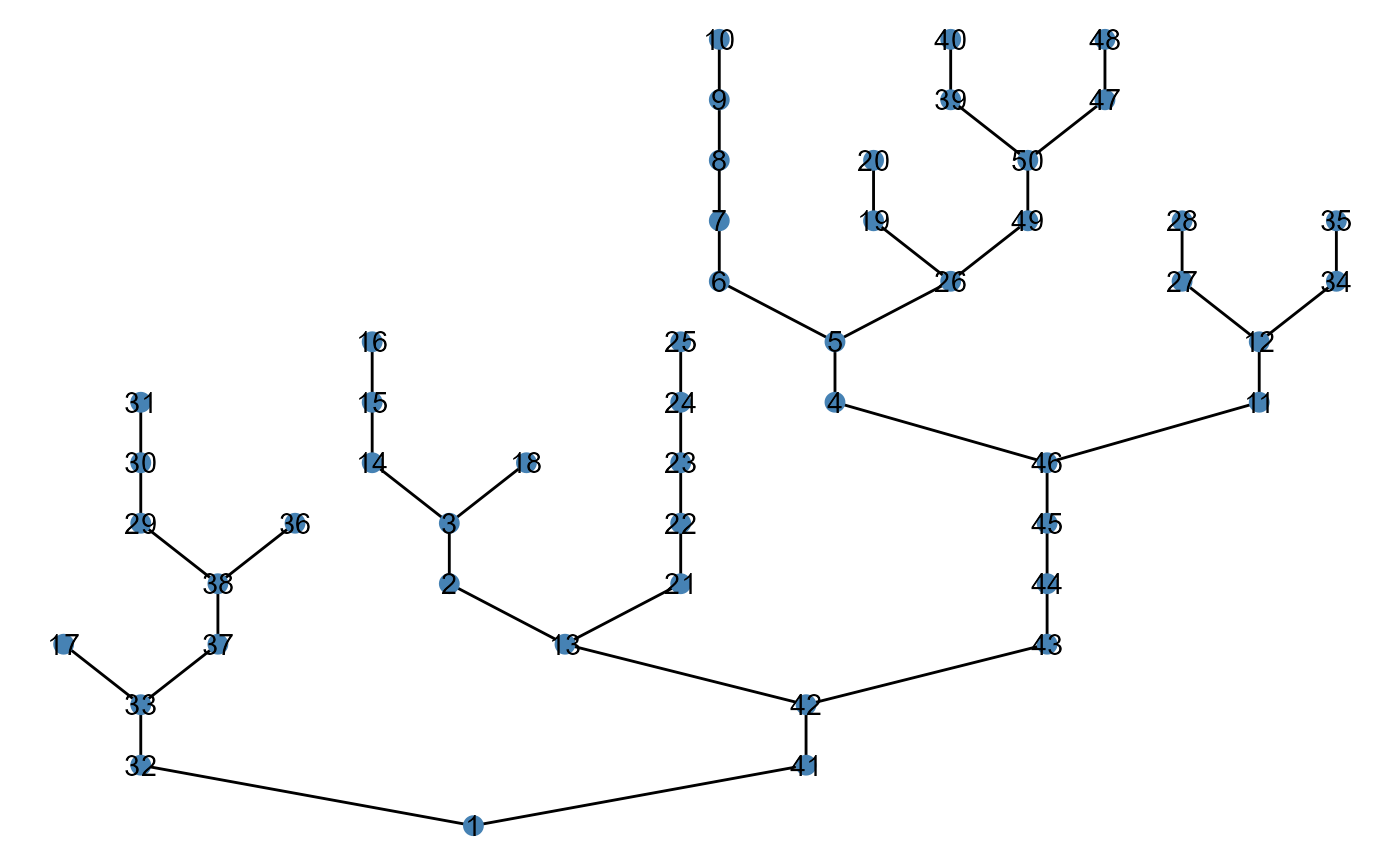
# number of upstream contributing patches
brnet(n_patch = 50,
      p_branch = 0.5) %>% 
  ggbrnet(patch_label = "n_upstream")

To change patch size, specify patch_size:

brnet(n_patch = 50,
      p_branch = 0.5) %>% 
  ggbrnet(patch_size = 1)

Customize: environment

Arguments: mean_env_source, sd_env_source, rho, sd_env_lon

Environmental values are generated as detailed below:

Environmental values for upstream terminal patches are drawn from a normal distribution as $z_h \sim N(\mu_{h}, \sigma_h^2)$ (arguments mean_env_source and sd_env_source).
Downstream environmental values are determined by an autoregressive process as $z_{down} \sim N(\rho z_{up}, \sigma_l^2)$ (argument sd_env_lon). At bifurcation patches (or confluence), the environmental value takes a weighted mean of the two contributing patches given the size of these patches $N_{up}$ (the number of upstream contributing patches): $z_{down} = \omega(\rho z_{up, 1} + \epsilon_1) + (1 - \omega)(\rho z_{up,2} + \epsilon_2)$ , where $\omega = \frac{N_{up,1}}{N_{up,1} + N_{up,2}}$ and $\epsilon \sim N(0, \sigma_l^2)$ .

Users may change the values of $\mu_h$ (default: mean_env_source = 0), $\sigma_h$ (sd_env_source = 1), $\rho$ (rho = 1), and $\sigma_l$ (sd_env_lon = 0.1). Increasing the value of sd_env_source leads to greater variation in environmental values at upstream terminals. The argument rho determines the strength of longitudinal autocorrelation (the greater the stronger autocorrelation). The argument sd_env_lon determines the strength of longitudinal environmental noise.

# with large variation at headwaters
brnet(n_patch = 50,
      p_branch = 0.5,
      sd_env_source = 3,
      sd_env_lon = 0.5,
      rho = 0.5) %>% 
  ggbrnet(patch_color = "env")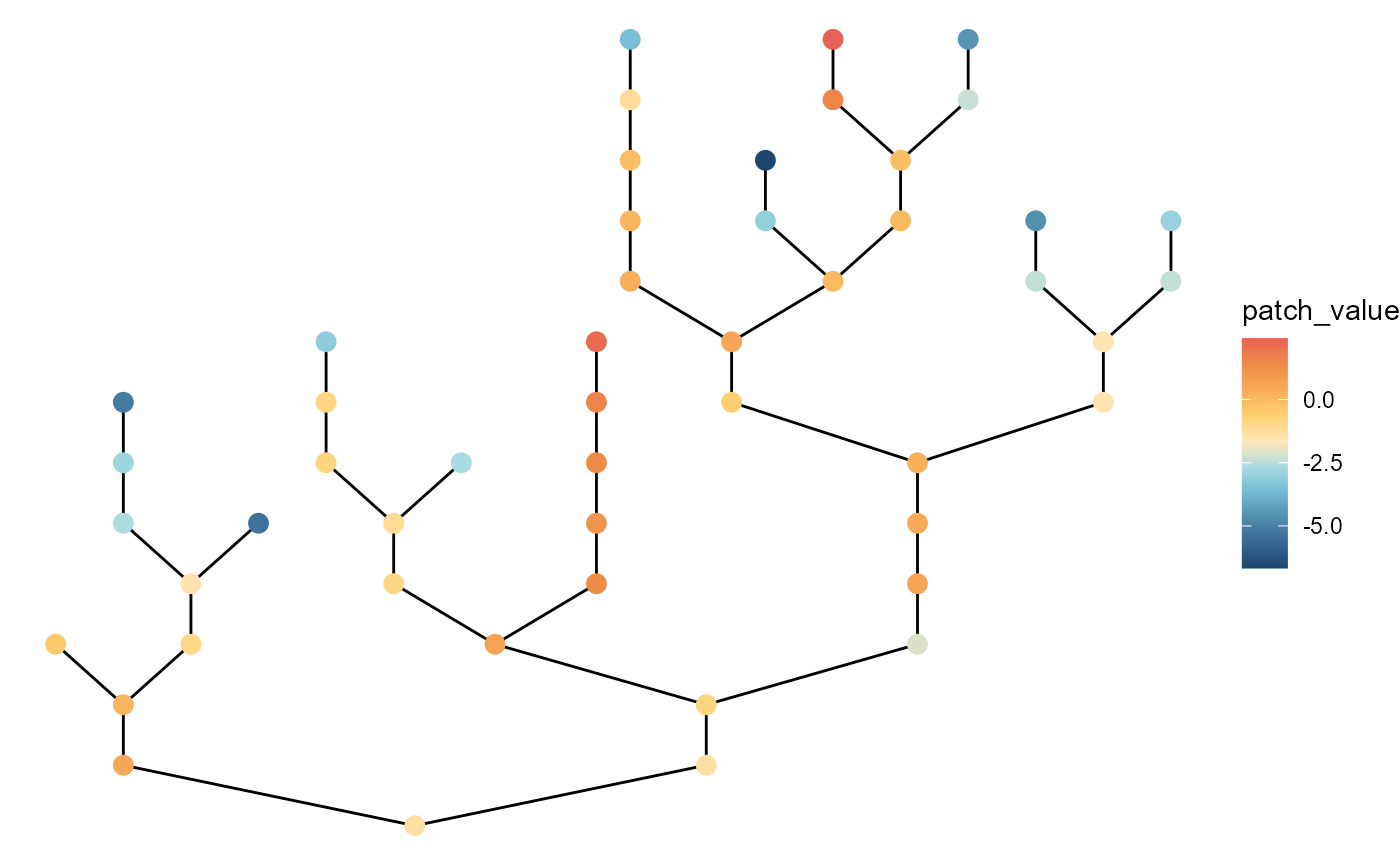

# large local variation with no headwater variation
brnet(n_patch = 50,
      p_branch = 0.5,
      sd_env_source = 0,
      sd_env_lon = 3,
      rho = 0.5) %>% 
  ggbrnet(patch_color = "env")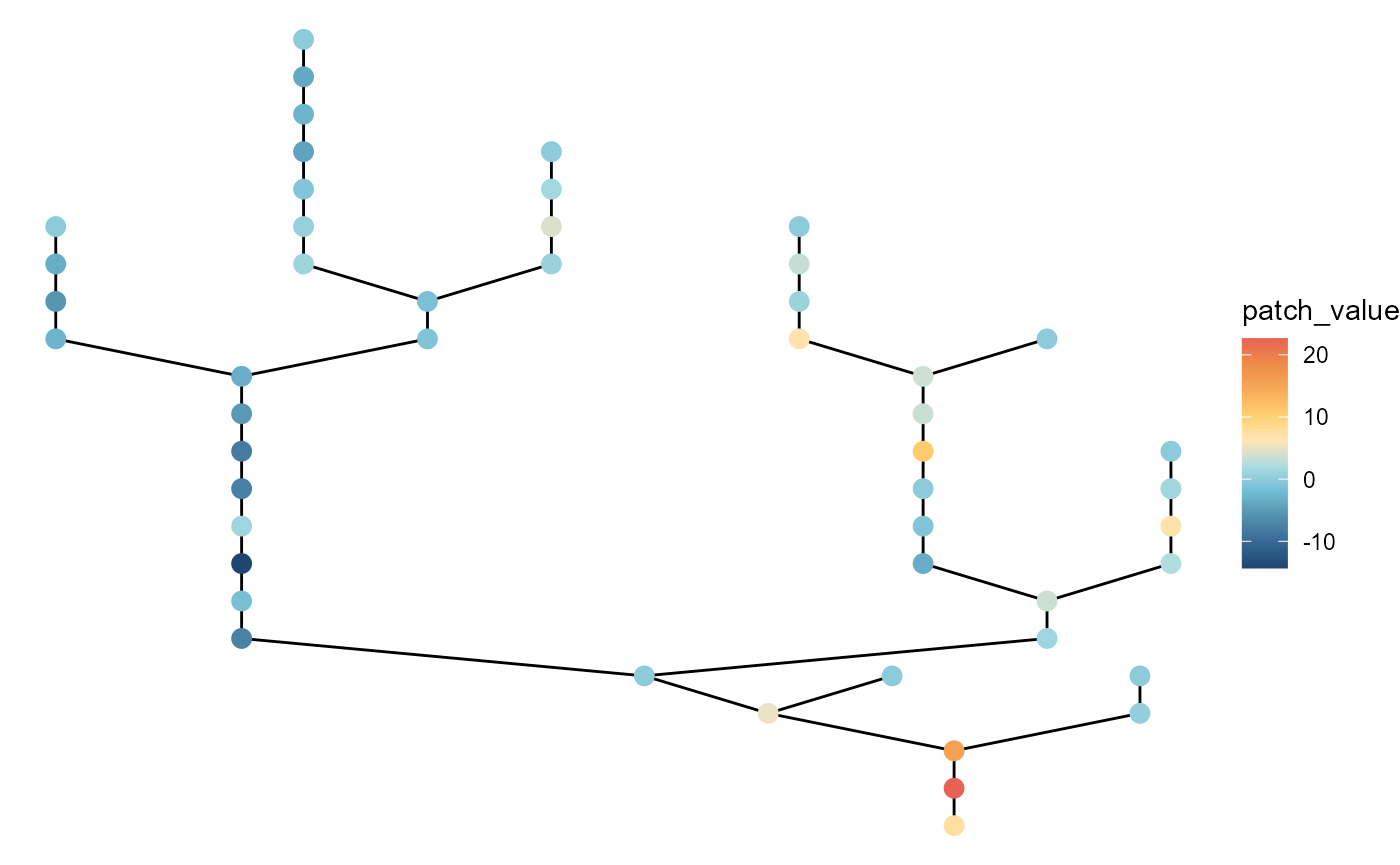

Customize: disturbance

Arguments: mean_disturb_source, sd_disturb_source , sd_disturb_lon

Disturbance values are generated as detailed below:

Disturbance levels for upstream terminal patches (i.e., patches with no upstream patch) are drawn from a normal distribution in a logit scale as $\text{logit}~m_h \sim N(\text{logit}~\mu_{m}, \sigma_{h,m}^2)$ .
Disturbance cascades downstream as in environmental values: $\text{logit}~m_{down} \sim N(\text{logit}~m_{up}, \sigma_{l,m}^2)$ . At bifurcation patches (or confluence), the disturbance value takes a weighted mean of the two contributing patches given the stream size of these patches $N_{up}$ (the number of upstream contributing patches): $\text{logit}~m_{down} = \omega(\text{logit}~m_{up, 1} + \epsilon_1) + (1 - \omega)(\text{logit}~ m_{up,2} + \epsilon_2)$ , where $\omega = \frac{N_{up,1}}{N_{up,1} + N_{up,2}}$ and $\epsilon \sim N(0, \sigma_{l,m}^2)$ .

Users may change the values of $\mu_{m}$ (mean_disturb_source), $\sigma_{h,m}$ (sd_disturb_source) and $\sigma_{l,m}$ (sd_disturb_lon).

# with large variation at headwaters
brnet(n_patch = 50,
      p_branch = 0.5,
      sd_disturb_source = 3,
      sd_disturb_lon = 0.5) %>% 
  ggbrnet(patch_color = "disturb")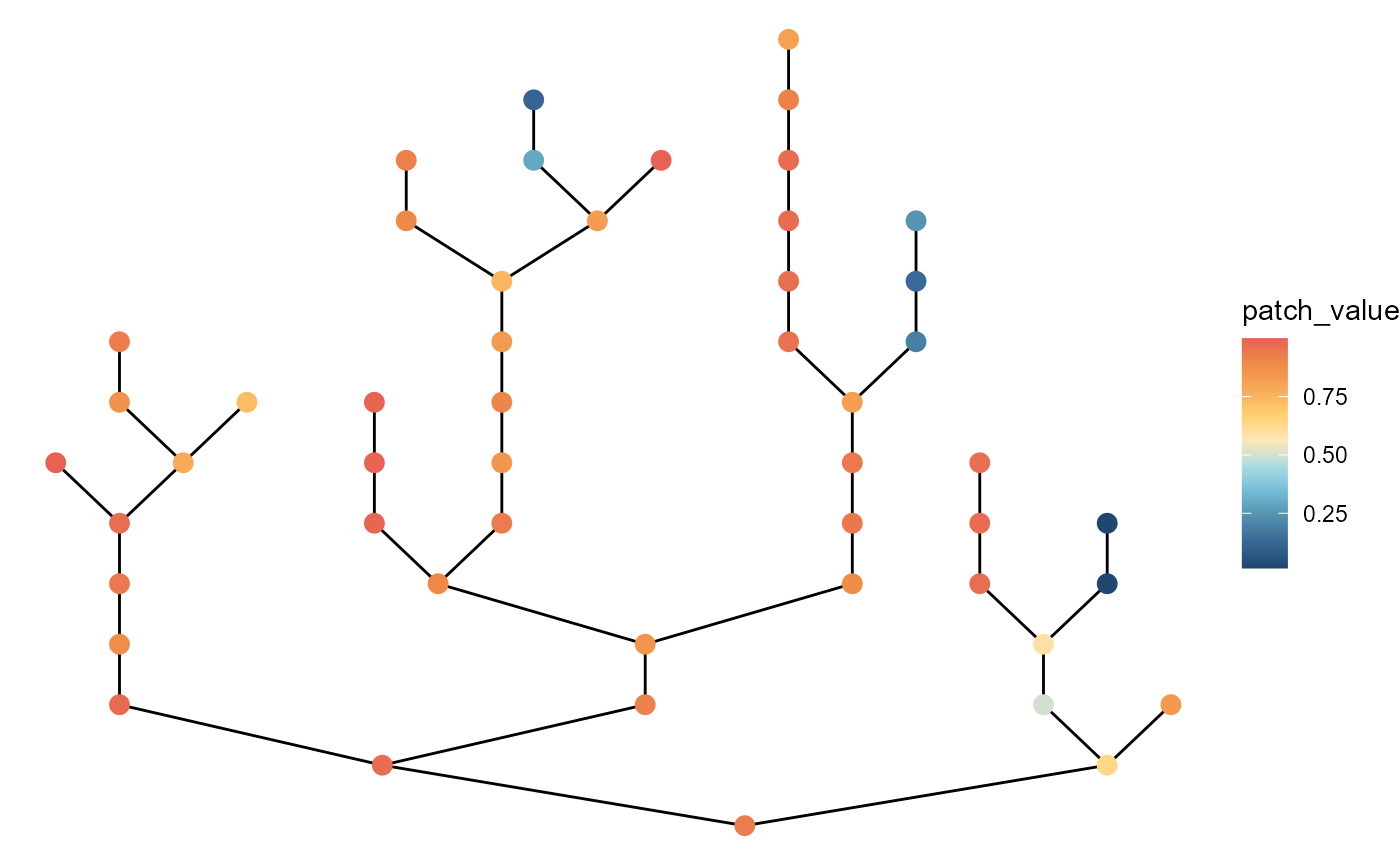

# with large local variation with no headwater variation
brnet(n_patch = 50,
      p_branch = 0.5,
      sd_disturb_source = 0,
      sd_disturb_lon = 3) %>% 
  ggbrnet(patch_color = "disturb")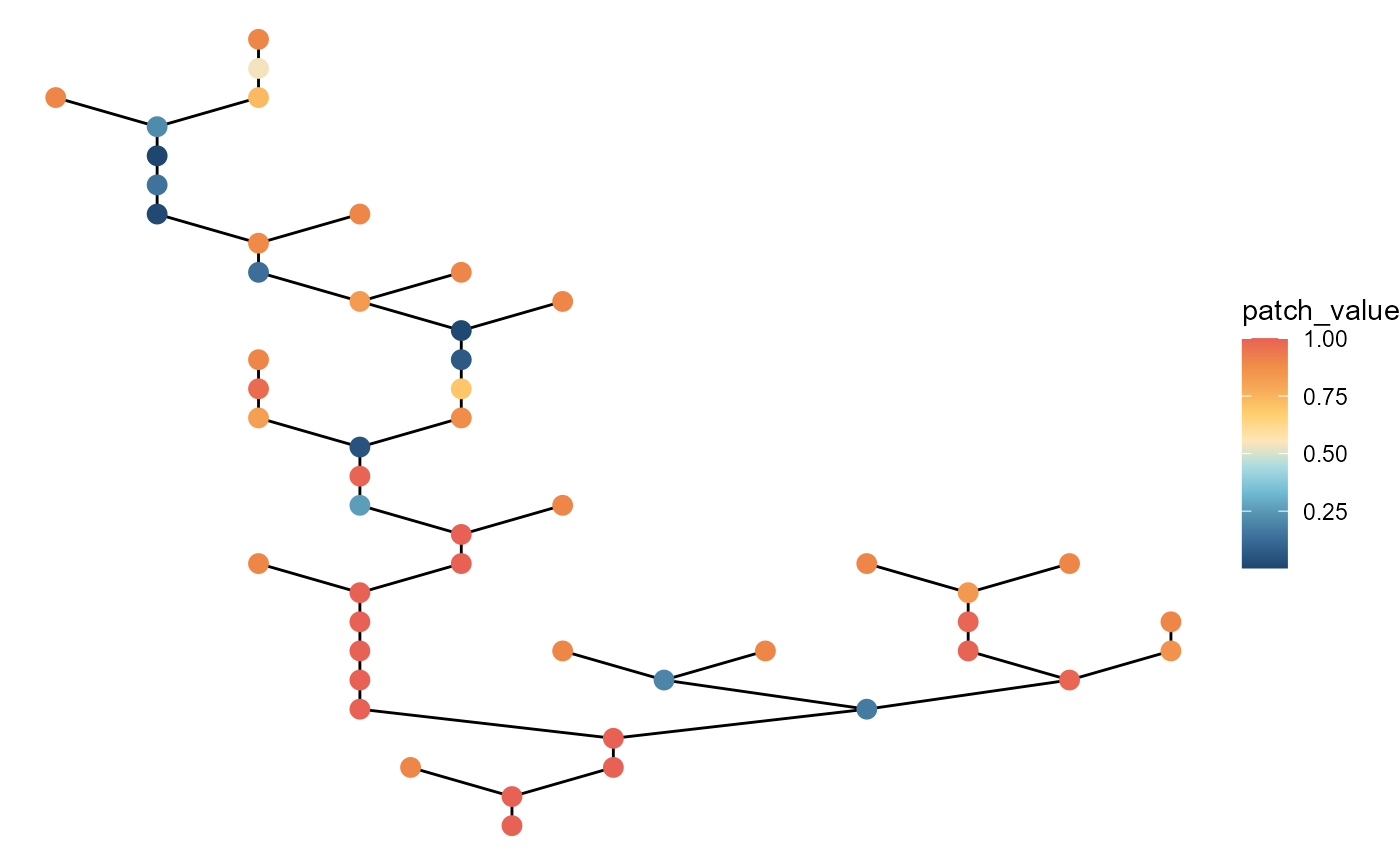

Customize: environmental pollutants

Arguments: x, n_source, p, q, pattern

From v.1.3.0, mcbrnet offers ptsource() function to simulate propagation of environmental pollutants in a branching network. ptsource() can specify:

x brnet() object
n_source number of point sources
p strength of downstream propagation
q strength of upstream propagation
pattern spatial pattern of point sources - "random", "cluster", "upstream", "downstream"

The function takes brnet() object as the first argument, so it’s compatible with pipe %>%. The concentration of pollutants has a value of 1.0 at point sources and decays with distance as $p^d$ in downstream ( $d=$ distance, $p=$ geometric coefficient of distance decay) and $q^d$ in upstream. For example, if a focal location is 3 patches downstream from the point source with $p = 0.8$ , the concentration would be $0.8^3 = 0.512$ . By setting different values of p and q, users can model the asymmetric propagation of environmental pollutants.

For example, the following script will add a new column impact that represents the concentration of hypothetical environmental pollutant:

y <- brnet(n_patch = 10) %>% 
  ptsource(n_source = 3,
           p = 0.8,
           q = 0) 

y$df_patch
#> # A tibble: 10 × 7
#>    patch_id impact point_source branch_id environment disturbance
#>       <int>  <dbl>        <dbl>     <dbl>       <dbl>       <dbl>
#>  1        1   2.36            1         1      0.163        0.964
#>  2        2   1.7             1         1      0.272        0.970
#>  3        3   0               0         5      0.473        0.879
#>  4        4   1               1         2      0.0756       0.972
#>  5        5   0               0         2      0.0314       0.974
#>  6        6   0               0         2      0.0124       0.979
#>  7        7   0               0         3     -0.586        0.995
#>  8        8   0               0         3     -0.525        0.994
#>  9        9   0               0         4      0.676        0.918
#> 10       10   0               0         4      0.783        0.908
#> # ℹ 1 more variable: n_patch_upstream <dbl>

Also, easy to visualize the spatial pattern of pollution with ggbrnet(). Just need to set patch_color = "impact".

brnet(n_patch = 30) %>% 
  ptsource(n_source = 3,
           p = 0.8,
           q = 0) %>% 
  ggbrnet(patch_color = "impact") +
  labs(color = "Impact")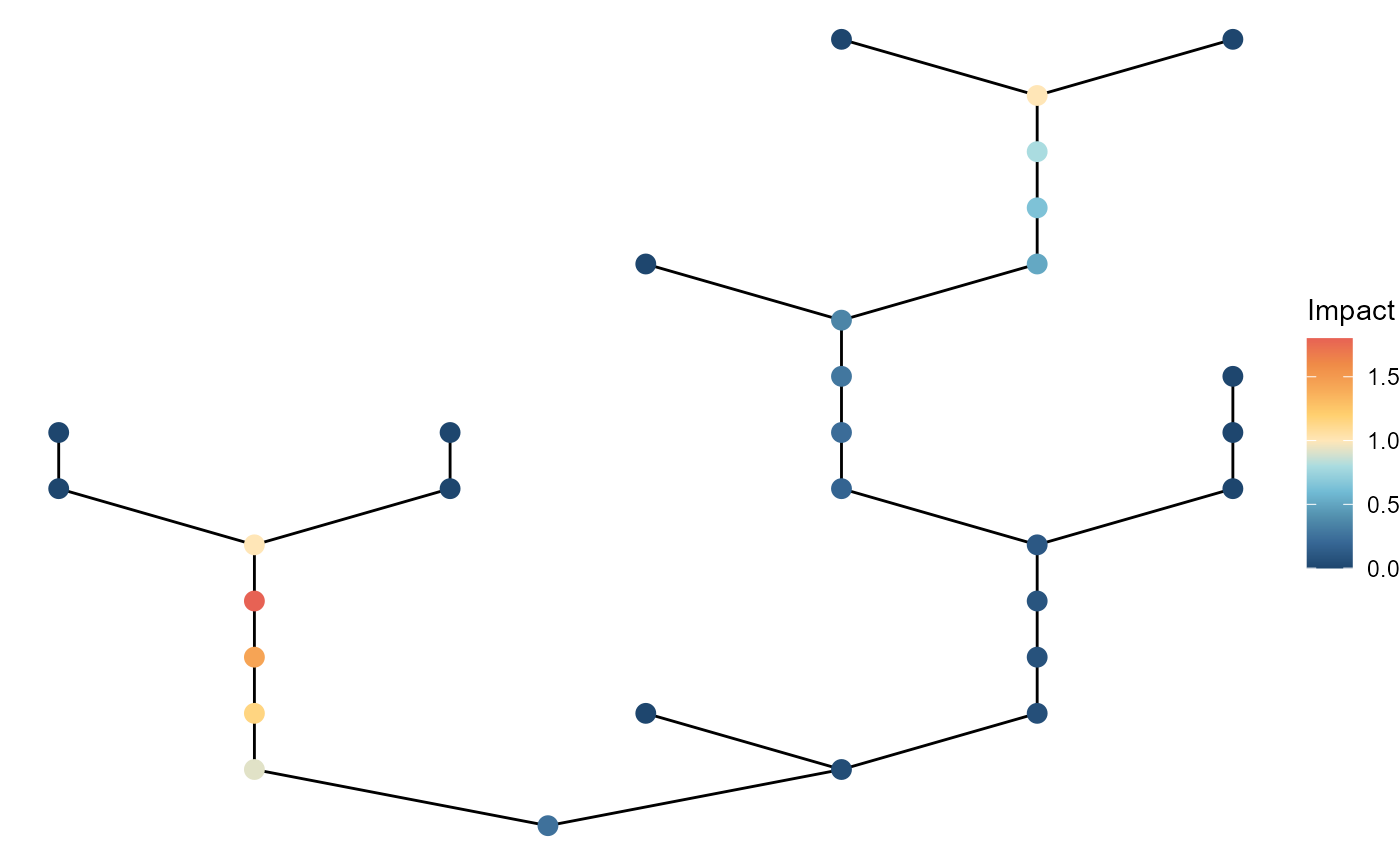

Finally, it is possible to specify the spatial pattern of point sources. By default, the function generates point sources at random, but it may be more realistic to have some spatial clusters.

The "cluster" pattern randomly pick one location as a the first point source, and the rest of point sources appear close to this initial point source:

brnet(n_patch = 30) %>% 
  ptsource(n_source = 3,
           p = 0.8,
           q = 0,
           pattern = "cluster") %>% 
  ggbrnet(patch_color = "impact") +
  labs(color = "Impact")

The "upstream" pattern pick point source locations from smaller tributaries (i.e., based on number of upstream patches), but not necessarily clustered:

brnet(n_patch = 30) %>% 
  ptsource(n_source = 3,
           p = 0.8,
           q = 0,
           pattern = "upstream") %>% 
  ggbrnet(patch_color = "impact") +
  labs(color = "Impact")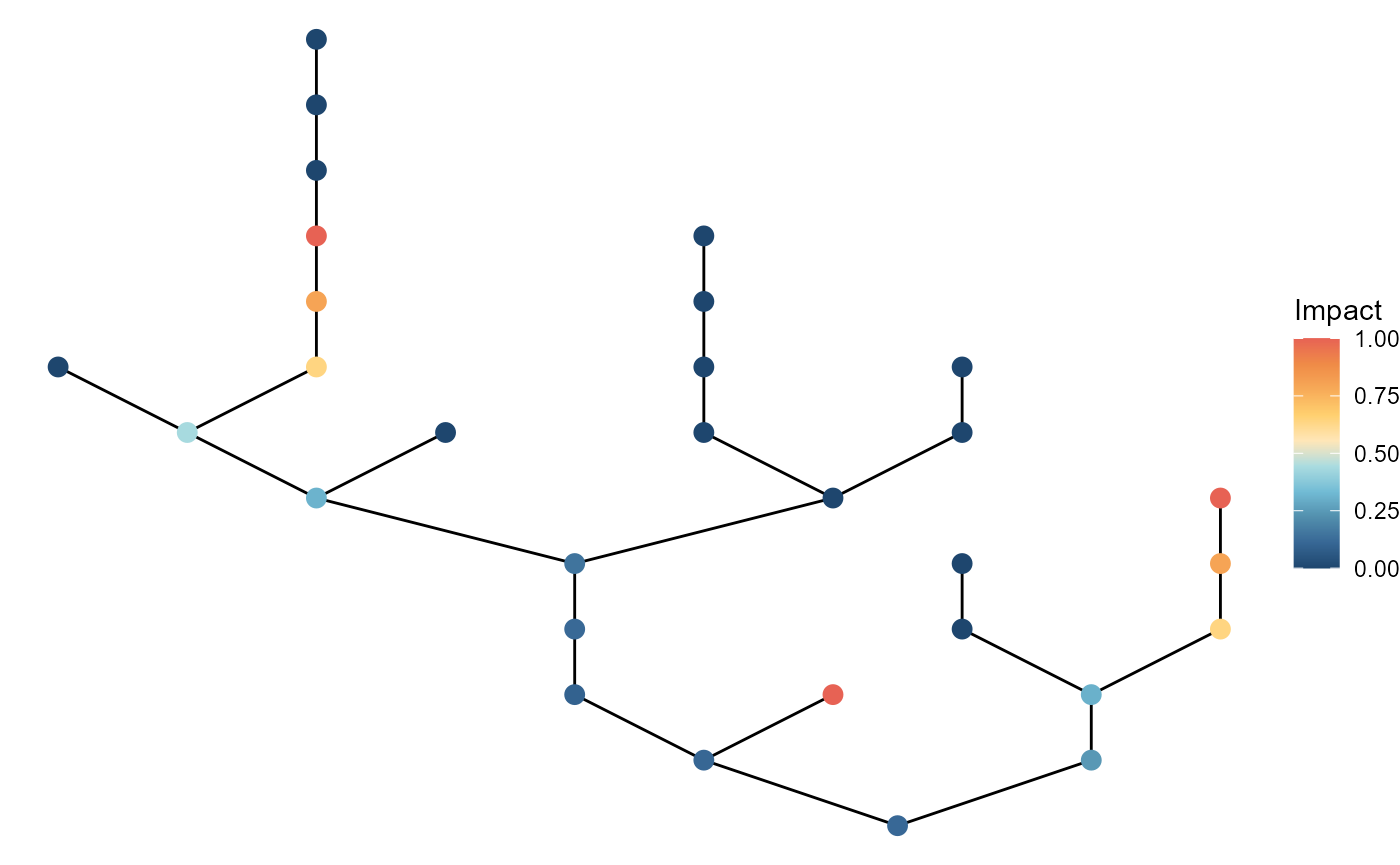

The "downstream" does the opposite (pick from larger streams):

brnet(n_patch = 30) %>% 
  ptsource(n_source = 3,
           p = 0.8,
           q = 0,
           pattern = "downstream") %>% 
  ggbrnet(patch_color = "impact") +
  labs(color = "Impact")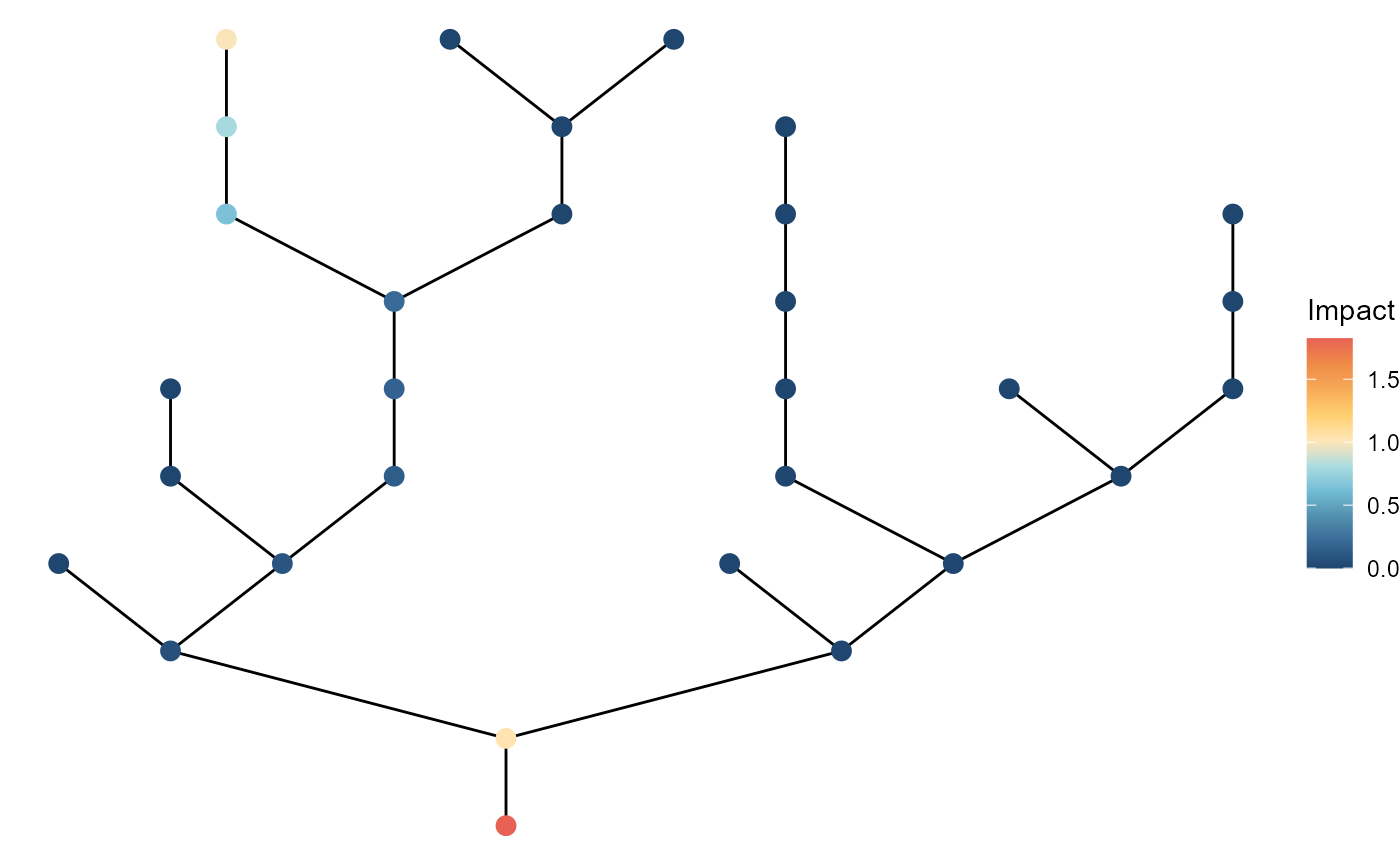

Customize: fragmentation

Arguments: x, rate, pattern, p, n_barrier

frgm() will impose fragmentation to a network. The function can specify:

x ‘brnet’ object or adjacency matrix
rate rate parameter of exponential dispersal kernel (i.e., species attribute). This parameter defines the result dispersal matrix.
pattern fragmentation pattern; either “random” (random location of fragmentation), “upstream” (upstream edges are more likely to be fragmented), or “downstream” (downstream edges are more likely to be fragmented).
p passability of fragmented edges (probability)
n_barrier number of barriers

The arguments p and n_barrier define the probability of traversing across an edge with a barrier and the number of total barriers , respectively. Passability can be different among barriers; in this case, the user must specify the passabilities of individual barriers separately (as a vector with length n_barrier). The barrier effect is cumulative. For example, if one passes two barriers A (passability = $p_A$ ) and B (passability $p_B$ ) when moving from a given node node to another node, the original movement probability $m$ will be reduced to $m p_Ap_B$ .

Just like ptsource(), this function will take an output from brnet() function but also accepts any adjacency matrix. ggbrnet() will help you visualize fragmented edges by specifying edge_alpha = "passability".

Example: random pattern:

brnet(n_patch = 30) %>%
  frgm(rate = 0.1,
       p = 0.1,
       n_barrier = 5,
       pattern = "random") %>%
  ggbrnet(edge_alpha = "passability")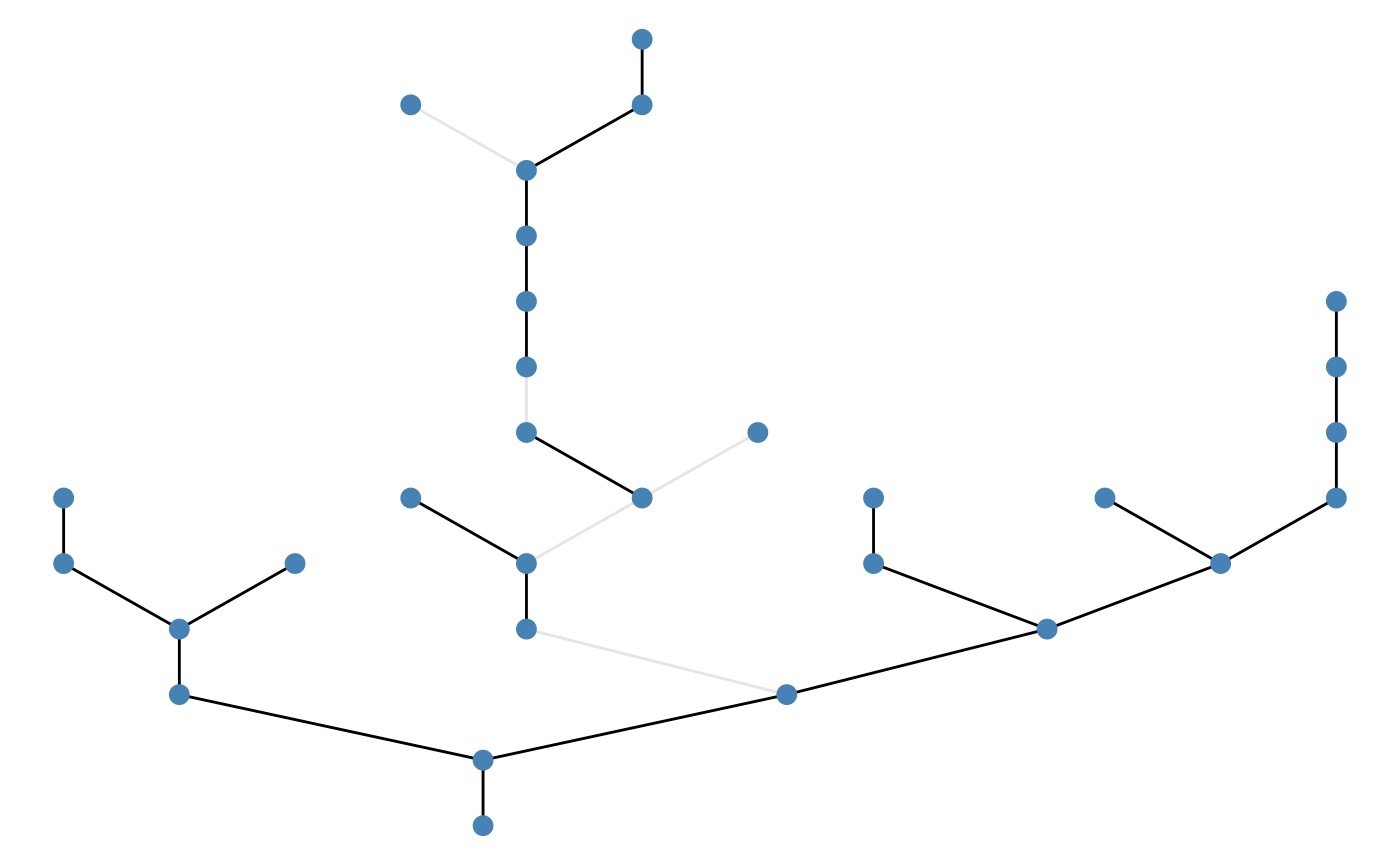

Example: upstream pattern:

brnet(n_patch = 30) %>%
  frgm(rate = 0.1,
       p = 0.1,
       n_barrier = 5,
       pattern = "upstream") %>%
  ggbrnet(edge_alpha = "passability")

Example: downstream pattern:

brnet(n_patch = 30) %>%
  frgm(rate = 0.1,
       p = 0.1,
       n_barrier = 5,
       pattern = "downstream") %>%
  ggbrnet(edge_alpha = "passability")