igpsim

Basic usage

igpsim() simulates tri-trophic food web dynamics with intraguild predation in space. The function employs a discrete time-series model (an extension of the Nicholson-Bailey model), which is detailed in Pomeranz et al. 2023. The food web dynamics are simulated through (1) local predator-prey interactions within a habitat patch, (2) immigration, and (3) emigration.

The function returns:

df_dynamics data frame containing simulated food web dynamics*.
- timestep: time-step.
- patch_id: patch ID.
- carrying_capacity: carrying capacity at each patch.
- disturbance: disturbance-induced mortality at patch x and time-step t.
- species: species ID.
- abundance: abundance of species i at patch x.
- fcl: food chain length
df_species data frame containing species attributes.
- species: species ID.
- mean_abundance: mean abundance (arithmetic) of species i across sites and time-steps.
- p_dispersal: dispersal probability of species i.
df_patch data frame containing patch attributes.
- patch_id: patch ID.
- fcl: temporal average of food chain length.
- carrying_capacity: carrying capacity at each patch.
- disturbance: disturbance-induced mortality at each patch.
df_int data frame containing interaction parameters.
- interaction: column identifying interaction pairs
- conv_eff: conversion efficiency
- attak_rate: attack rate
- handling_time: handling time
df_xy_coord xy coordinates for habitat patches (NULL when distance_matrix or dispersal_matrix is provided)
distance_matrix distance matrix used in the simulation.

Quick start

The following script simulates tri-trophic dynamics with n_patch = 5, which assumes five habitat patches randomly distributed over a square space. By default, igpsim() simulates food web dynamics with 200 warm-up (initialization with species introductions: n_warmup), 200 burn-in (burn-in period with no species introductions: n_burnin), and 1000 time-steps for records (n_timestep).

igp <- igpsim(n_patch = 5)

As in mcsim(), the simulated dynamics can be visualized by plot = TRUE, which will show five sample patches:

igp <- igpsim(n_patch = 5, plot = TRUE)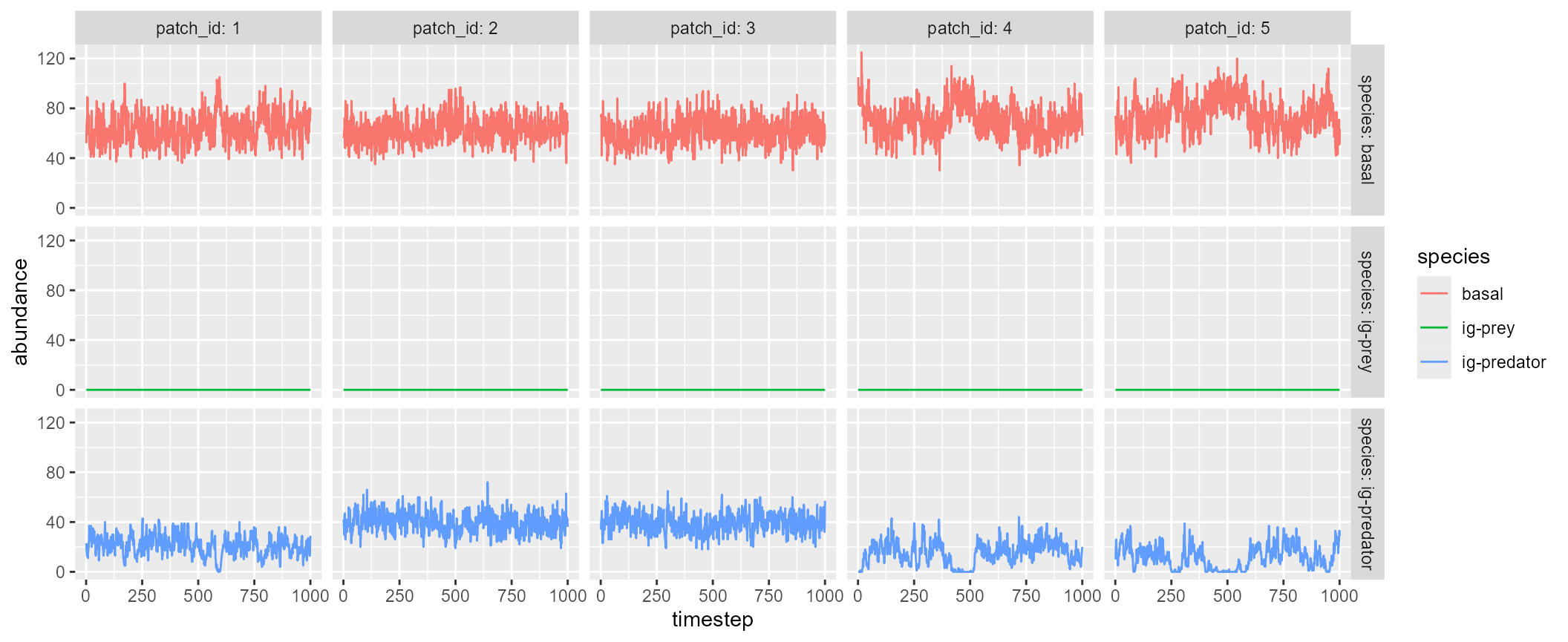

A named list of return values:

igp
#> $df_dynamics
#> # A tibble: 15,000 × 7
#>    timestep patch_id carrying_capacity disturbance species     abundance   fcl
#>       <dbl>    <dbl>             <dbl>       <dbl> <fct>           <dbl> <dbl>
#>  1        1        1               100           0 basal              52     2
#>  2        1        1               100           0 ig-prey             0     2
#>  3        1        1               100           0 ig-predator        23     2
#>  4        1        2               100           0 basal              56     2
#>  5        1        2               100           0 ig-prey             0     2
#>  6        1        2               100           0 ig-predator        42     2
#>  7        1        3               100           0 basal              73     2
#>  8        1        3               100           0 ig-prey             0     2
#>  9        1        3               100           0 ig-predator        34     2
#> 10        1        4               100           0 basal             105     1
#> # ℹ 14,990 more rows
#> 
#> $df_species
#> # A tibble: 3 × 3
#>   species     mean_abundance p_dispersal
#>   <fct>                <dbl>       <dbl>
#> 1 basal                 66.6         0.1
#> 2 ig-prey                0           0.1
#> 3 ig-predator           25.4         0.1
#> 
#> $df_patch
#> # A tibble: 5 × 4
#>   patch_id   fcl carrying_capacity disturbance
#>      <dbl> <dbl>             <dbl>       <dbl>
#> 1        1  2.00               100           0
#> 2        2  2                  100           0
#> 3        3  2                  100           0
#> 4        4  1.92               100           0
#> 5        5  1.85               100           0
#> 
#> $df_int
#> # A tibble: 3 × 4
#>   interaction            conv_eff attack_rate handling_time
#>   <chr>                     <dbl>       <dbl>         <dbl>
#> 1 ig-prey on basal            0.9        0.05           0.5
#> 2 ig-predator on basal        0.9        0.05           0.5
#> 3 ig-predator on ig-prey      0.9        0.05           0.5
#> 
#> $df_xy_coord
#> # A tibble: 5 × 2
#>   x_coord y_coord
#>     <dbl>   <dbl>
#> 1    9.09    1.76
#> 2    9.21    6.38
#> 3    8.02    8.01
#> 4    2.01    8.72
#> 5    1.98    3.39
#> 
#> $distance_matrix
#>          1        2        3        4        5
#> 1 0.000000 4.620888 6.343422 9.929323 7.294714
#> 2 4.620888 0.000000 2.021374 7.569156 7.819384
#> 3 6.343422 2.021374 0.000000 6.047221 7.598888
#> 4 9.929323 7.569156 6.047221 0.000000 5.327876
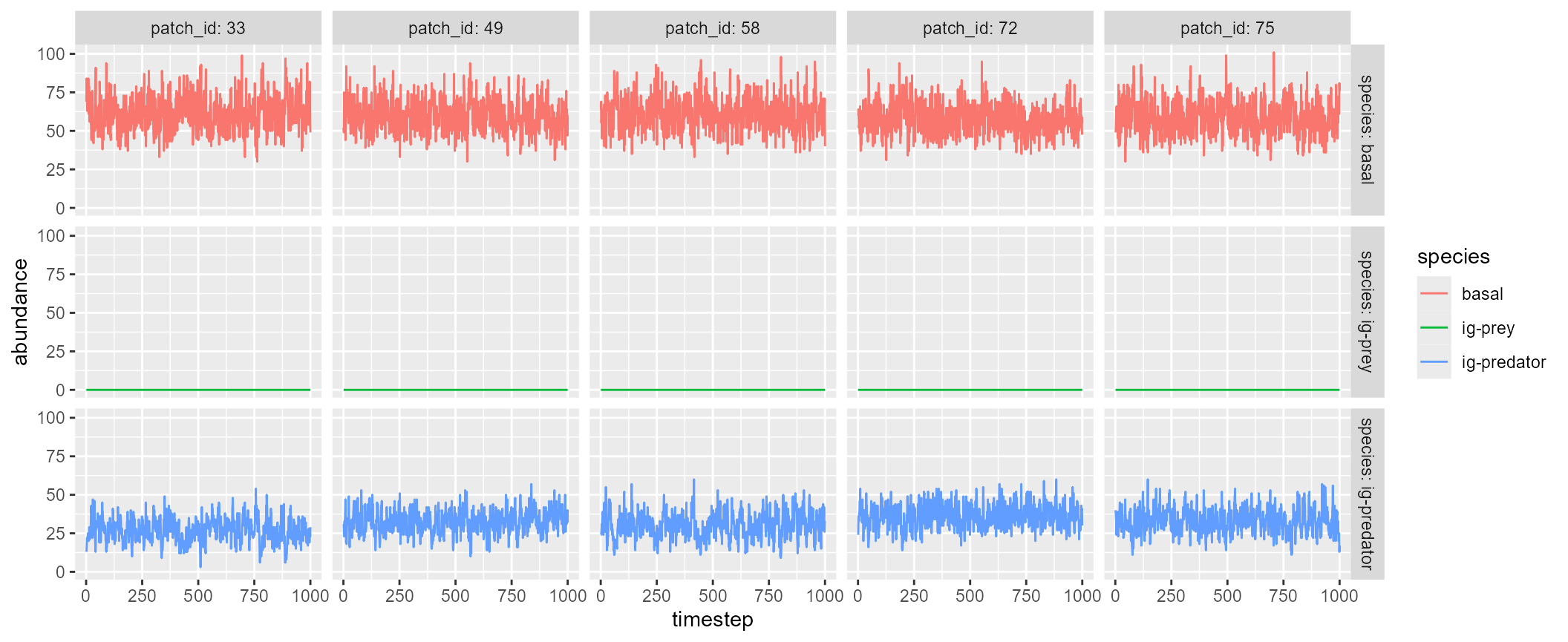
#> 5 7.294714 7.819384 7.598888 5.327876 0.000000

Custom: `brnet()` + `igpsim()`

brnet() outputs are compatible with igpsim(). For example, .$distance_matrix may be used to inform arguments in igpsim(). By providing the distance matrix, the following script will simulate food web dynamics in a random branching network produced by brnet() function:

patch <- 100

net <- brnet(n_patch = patch,
             p_branch = 0.5)

igp <- with(net,
            igpsim(n_patch = patch,
                   distance_matrix = distance_matrix,
                   plot = TRUE)
            )

Custom: parameter detail

Users can tweak (1) food web attributes, (2) patch attributes, and (3) landscape structure.

Food web attributes

Arguments: r_b, conv_eff, attack_rate, handling_time, s

Food web attributes are determined based on the maximum reproductive rate of the basal species (r_b), conversion efficiency conv_eff, attack rate attack_rate, handling time handling_time, and switching parameter s.

Basal species – r_b is one of the parameters defining the population growth of the basal species, modeled as follows:

$B_{t} = \frac{B_{t-1}r_b}{1 + \frac{r_b - 1}{K}B_{t-1}},$

where $B_t$ is the abundance of the basal species at time $t$ , $r_b$ is the maximum growth rate (= r_b), and $K$ is the carrying capacity (= carrying_capacity; see Patch attributes). The parameters $r_b$ and $K$ may vary by habitat; to model such variations, users may supply vectors of r_b and carrying_capacity, whose length is equal to n_patch. The function assumes these values are supplied in order of patch 1, 2, 3, …, n_patch. Thus, care must be taken to match this order with those in, e.g., distance_matrix.

Consumers (intraguild prey and predator) – The predator-prey interactions are modeled with the Nicholson-Bailey model, which was extended to account for intraguild predation (see Pomeranz et al. 2023, Ecosphere; equations 5 – 9 for details). The function assumes the discrete version of the Holling’s Type-II functional response, in which attack rate (atttack_rate) and handling time (handling_time) define the survival function $f(\cdot)$ of the prey as follows:

$\begin{aligned} f(B, C) &= \exp(-\frac{a_{BC}C}{1 + a_{BC}h_{BC}B}) &&\text{C on B},\\ f(B, P) &= \exp(-\frac{(1 + \phi)a_{BP}P}{1 + a_{BP}h_{BP}B}) &&\text{P on B},\\ f(C, P) &= \exp(-\frac{(1 - \phi)a_{CP}P}{1 + a_{CP}h_{CP}C}) &&\text{P on C},\\ \end{aligned}$

where $C$ and $P$ are the abundances of intraguild prey and predator, respectively, $a_{ij}$ the attack rate of consumer $j$ on prey $i$ (= attack_rate), and $h_{ij}$ the handling time (= handling_time). If these arguments are supplied as scalars, then the function assumes the constant values for all the interactions (i.e., $a_{BC} = a_{BP} = a_{CP} = const.$ and $h_{BC} = h_{BP} = h_{CP} = const.$ ). Where appropriate, users may apply different values to these by supplying vectors; in this case, the function assumes the parameter values appear in order of $a_{BC}$ ( $h_{BC}$ ), $a_{BP}$ ( $h_{BC}$ ), and $a_{CP}$ ( $h_{CP}$ ). The parameter $\phi$ quantifies the switching tendency of the intraguild predator, defined as follows:

$\phi = \frac{s(B - C)}{B+C}$

The parameter $s$ (= s) determines the likelihood of switching to the basal species, with higher values of $s$ indicating the greater switching tendency to the basal species. Lastly, conversion efficiency (= conv_eff) quantifies the effectiveness of consumers transforming the capture prey into consumer’s abundance. conv_eff must be a scalar (supply identical values to all the interactions) or must be supplied in order of $BC$ , $BP$ , and $CP$ .

Note that the function assumes the following order of ecological events: $B$ ’s reproduction $\rightarrow$ $C$ ’s predation on $B$ $\rightarrow$ $C$ ’s reproduction $\rightarrow$ $P$ ’s predation on $B$ and $C$ $\rightarrow$ $P$ ’s reproduction.

Patch attributes

Arguments: carrying_capacity p_disturb, i_disturb, phi_disturb

Patch attributes are characterized by carrying capacity (= carrying_capacity) and disturbance (probability of occurrence = p_disturb, disturbance intensity = i_disturb, temporal precision of disturbance intensity = phi_disturb). carrying_capacity and i_disturb can be supplied as patch specific values, provided that the vector lengths match n_patch. The other arguments p_disturb and phi_disturb should be given as scalars. p_disturb controls how often disturbance occurs, while phi_disturb regulates the temporal variability of the disturbance intensity when it occurs (greater values of phi_disturb indicating less temporal variability).

Note that disturbance events in this function is designed to resemble regional disturbance, which affects all habitat patches when it occurs. Thus, disturbance heterogeneity within a landscape should be introduced through i_disturbance argument if desired.

Landscape attributes

Arguments: xy_coord, distance_matrix, landscape_size, theta

See Article for mcsim()

Others

Arguments: n_warmup, n_burnin, n_timestep