5 Multiple-Group Comparison

The t-test is used to compare two groups, but when there are more than two groups, ANOVA (Analysis of Variance) is employed. ANOVA allows for simultaneous comparison of means among multiple groups to determine if there are statistically significant differences. ANOVA uses the following steps:

Partition the total variability into between-group and within-group components.
Define a test statistic as a ratio of between-group variability to within-group variability (F statistic).
Define a probability distribution of F-statistic under the null hypothesis.
Estimate the probability of yielding greater the observed test statistic.

If appropriate, post-hoc tests can be conducted to identify specific differing groups.

Key words: F-statistic, Sum of Squares

5.1 Partition the Variability

The first step is to determine what aspect to examine. In the case of a t-test, we focus on the difference in sample means between groups. One might initially consider conducting t-tests for all possible combinations. However, this approach leads to a problem known as the multiple comparisons problem. Hence, this is not a viable option. Therefore, we need to explore the data from a different perspective.

To facilitate learning, let’s once again utilize the lake fish data (download here), but this time we have three lakes in our analysis:

df_anova <- read_csv("data_raw/data_fish_length_anova.csv")
distinct(df_anova, lake)

## # A tibble: 3 × 1
##   lake 
##   <chr>
## 1 a    
## 2 b    
## 3 c

Visualization can be helpful in understanding how the data is distributed. While mean \(\pm\) SD is perfectly fine here, let me use a violin plot to show a different way of visualization.

# geom_violin() - function for violin plots
# geom_jitter() - jittered points

df_anova %>% 
  ggplot(aes(x = lake,
             y = length)) +
  geom_violin(draw_quantiles = 0.5, # draw median horizontal line
              alpha = 0.2) + # transparency
  geom_jitter(alpha = 0.2) # transparency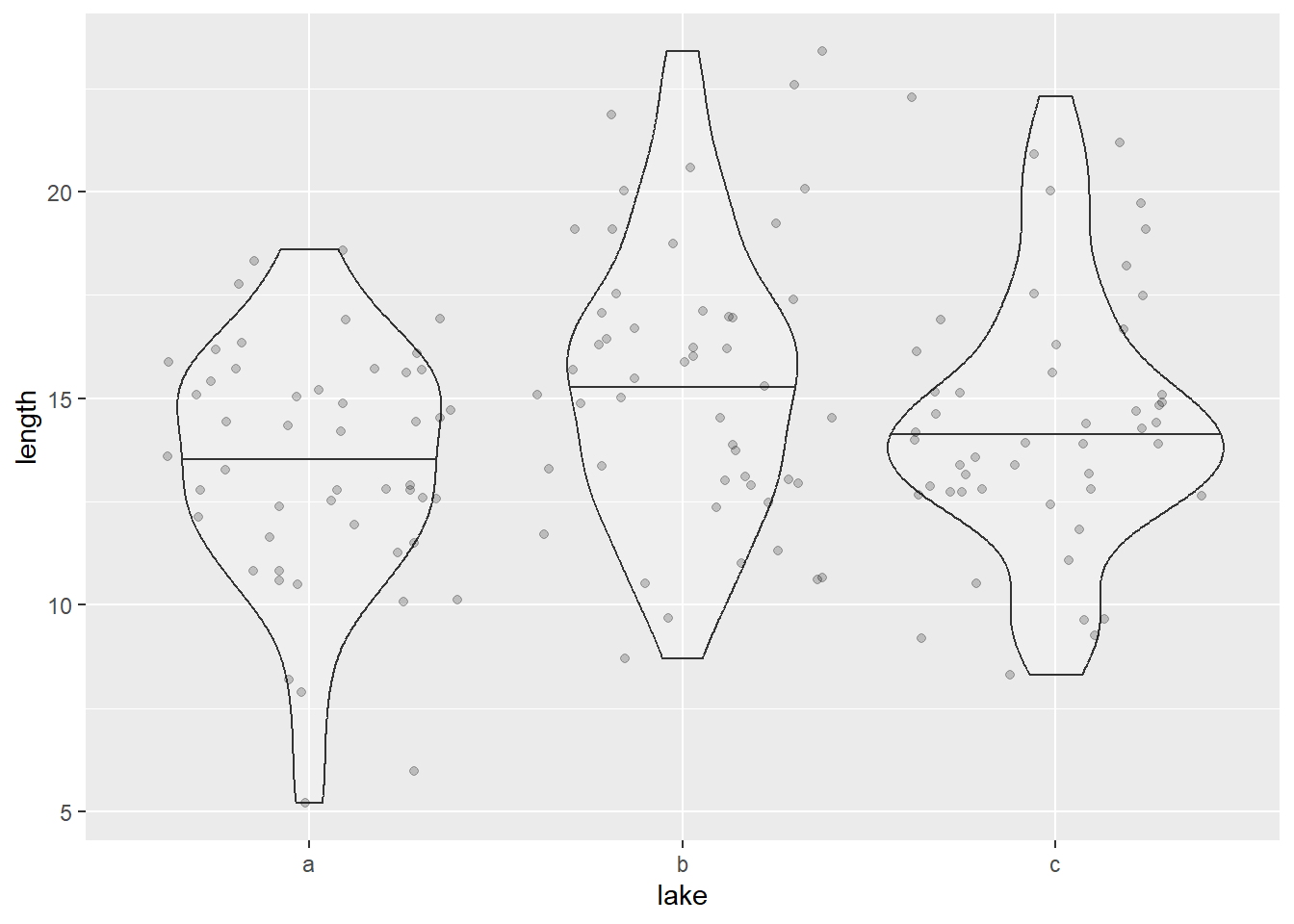

Figure 5.1: Violin plot for fish length in three lakes.

It appears that Lake b exhibits a larger average body size compared to the other lakes. One approach to quantifying this difference between groups is by examining the ratio of between-group variability to within-group variability. If we observe a greater between-group variability relative to within-group variability, it suggests that the differences among the groups are substantial. In other words, much of the observed variation is explained by the group structure (lake).

Let me denote between-group and within-group variability as \(S_b\) and \(S_w\), respectively, which are defined as follows:

\[ \begin{aligned} S_b &= \sum_g \sum_i (\hat{\mu}_{g(i)} - \hat{\mu})^2\\ S_w &= \sum_g \sum_i (x_{i} - \hat{\mu}_{g(i)})^2 \end{aligned} \]

The double summation \(\sum_g \sum_i\) might scare you, but no worries. We can decompose this equation into two steps.

5.1.1 Between-group variability

Let me first consider \(S_b = \sum_g \sum_i (\hat{\mu}_{g(i)} - \hat{\mu})^2\). In this equation, \(\hat{\mu}\) is the overall mean of the fish length and \(\hat{\mu}_{g(i)}\) is the group-mean in a given lake (\(g \in \{a, b, c\}\)). Let’s perform this estimation in R:

# estimate overall mean
mu <- mean(df_anova$length)

# estimate group means and sample size each
df_g <- df_anova %>% 
  group_by(lake) %>% 
  summarize(mu_g = mean(length), # mean for each group
            dev_g = (mu_g - mu)^2, # squared deviation for each group
            n = n()) # sample size for each group

print(df_g)

## # A tibble: 3 × 4
##   lake   mu_g   dev_g     n
##   <chr> <dbl>   <dbl> <int>
## 1 a      13.4 1.12       50
## 2 b      15.4 0.997      50
## 3 c      14.5 0.00344    50

In the column dev_g, we estimated \((\hat{\mu}_{g(i)} - \hat{\mu})^2\). We must sum over \(i\) (fish individual) to get the variability in each lake (\(\sum_i (\hat{\mu}_{g(i)} - \hat{\mu})^2\)). Since \(\hat{\mu}_{g(i)}\) is constant in each lake, we can simply multiply dev_g with sample size n in each lake:

df_g <- df_g %>% 
  mutate(ss = dev_g * n)

print(df_g)

## # A tibble: 3 × 5
##   lake   mu_g   dev_g     n     ss
##   <chr> <dbl>   <dbl> <int>  <dbl>
## 1 a      13.4 1.12       50 55.9  
## 2 b      15.4 0.997      50 49.9  
## 3 c      14.5 0.00344    50  0.172

Sum over \(g\) (lake) to get \(S_b\).

s_b <- sum(df_g$ss)
print(s_b)

## [1] 105.9365

5.1.2 Within-group variability

We can follow the same steps to estimate the within-group variability \(S_w = \sum_g \sum_i (x_{i} - \hat{\mu}_{g(i)})^2\). Let’s estimate \((x_{i} - \hat{\mu}_{g(i)})^2\) first:

df_i <- df_anova %>% 
  group_by(lake) %>% 
  mutate(mu_g = mean(length)) %>% # use mutate() to retain individual rows
  ungroup() %>% 
  mutate(dev_i = (length - mu_g)^2) # deviation from group mean for each fish

You can take a look at group-level data with the following code; the column mu_g contains group-specific means of fish length, and dev_i contains \((x_i - \hat{\mu}_{g(i)})^2\):

# filter() & slice(): show first 3 rows each group
print(df_i %>% filter(lake == "a") %>% slice(1:3))

print(df_i %>% filter(lake == "b") %>% slice(1:3))

print(df_i %>% filter(lake == "c") %>% slice(1:3))

Sum over \(i\) in each lake \(g\) (\(\sum_i (x_i - \hat{\mu}_{g(i)})^2\)):

df_i_g <- df_i %>% 
  group_by(lake) %>% 
  summarize(ss = sum(dev_i))

print(df_i_g)

## # A tibble: 3 × 2
##   lake     ss
##   <chr> <dbl>
## 1 a      417.
## 2 b      565.
## 3 c      486.

Then sum over \(g\) to get \(S_w\):

s_w <- sum(df_i_g$ss)
print(s_w)

## [1] 1467.645

5.1.3 Variability to Variance

I referred to \(S_b\) and \(S_w\) as “variability,” which essentially represents the summation of squared deviations. To convert them into variances, we can divide them by appropriate numbers. In Chapter 2, I mentioned that the denominator for variance is the sample size minus one. The same principle applies here, but with caution.

For the between-group variability, denoted as \(S_b\), the realized sample size is the number of groups, \(N_g\), which in this case is three (representing the number of lakes). Therefore, we divide by three minus one to obtain an unbiased estimate of the between-group variance, denoted as \(\hat{\sigma}_b^2\):

\[ \hat{\sigma}^2_b = \frac{S_b}{N_g-1} \]

# n_distinct() count the number of unique elements
n_g <- n_distinct(df_anova$lake)
s2_b <- s_b / (n_g - 1)
print(s2_b)

## [1] 52.96827

Meanwhile, we need to be careful when estimating the within-group variance. Since the within-group variance is measured at the individual level, the number of data used is equal to the number of fish individuals. Yet, we subtract the number of groups – while the rationale behind this is beyond the scope, we are essentially accounting for the fact that some of the degrees of freedom are “used up” in estimating the group means. As such, we estimate the within-group variance \(\hat{\sigma}^2_w\) as follows:

\[ \hat{\sigma}^2_w = \frac{S_w}{N-N_g} \]

s2_w <- s_w / (nrow(df_anova) - n_g)
print(s2_w)

## [1] 9.983982

5.2 Test Statistic

5.2.1 F-statistic

In ANOVA, we use F-statistic – the ratio of between-group variability to within-group variability. The above exercise was essentially performed to yield this test statistic:

\[ F = \frac{\text{between-group variance}}{\text{within-group variance}} = \frac{\hat{\sigma}^2_b}{\hat{\sigma}^2_w} \]

f_value <- s2_b / s2_w
print(f_value)

## [1] 5.305325

The F-statistic in our data was calculated to be 5.31. This indicates that the between-group variance is approximately five times higher than the within-group variance. While this difference appears significant, it is important to determine whether it is statistically substantial. To make such a claim, we can use the Null Hypothesis as a reference.

5.2.2 Null Hypothesis

The F-statistic follows an F-distribution when there is no difference in means among the groups. Therefore, the null hypothesis we are considering in our example is that the means of all groups are equal, represented as \(\mu_a = \mu_b = \mu_c\). It’s worth noting that the alternative hypotheses can take different forms, such as \(\mu_a \ne \mu_b = \mu_c\), \(\mu_a = \mu_b \ne \mu_c\), or \(\mu_a \ne \mu_b \ne \mu_c\). ANOVA, however, is unable to distinguish between these alternative hypotheses.

The degrees of freedom in an F-distribution are determined by two parameters: \(N_g - 1\) and \(N - N_g\). To visualize the distribution, you can utilize thedf() function. Similar to the t-test, we can plot the F-distribution and draw a vertical line to represent the observed F-statistic. This approach allows us to assess the position of the observed F-statistic within the distribution and determine the associated p-value.

x <- seq(0, 10, by = 0.1)
y <- df(x = x, df1 = n_g - 1, df2 = nrow(df_anova) - n_g)

tibble(x = x, y = y) %>% 
  ggplot(aes(x = x,
             y = y)) + 
  geom_line() + # F distribution
  geom_vline(xintercept = f_value,
             color = "salmon") # observed F-statistic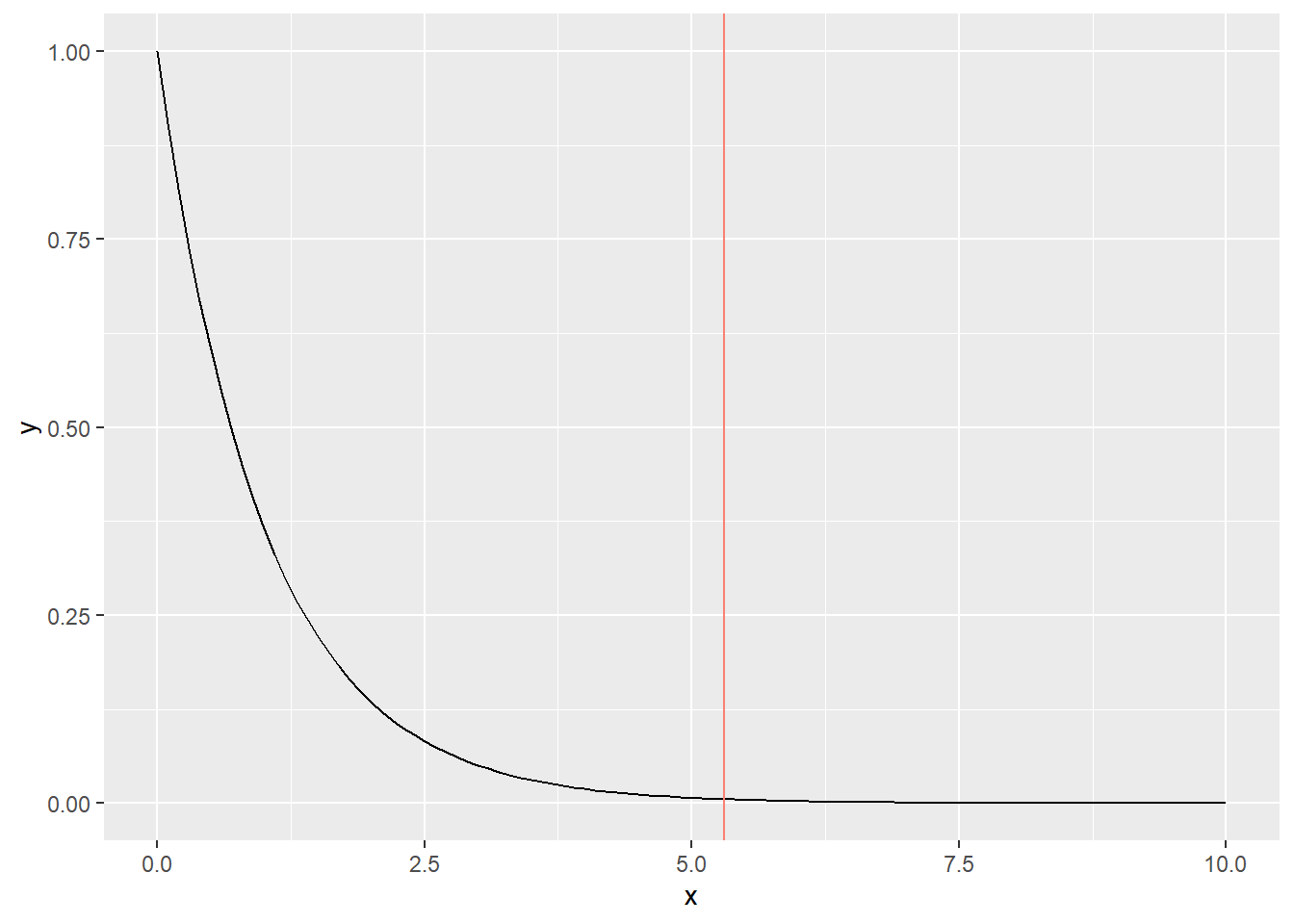

Figure 5.2: F-distribution. The vertical red line denotes the observed F-statistic.

Unlike t-statistics, F-statistics can take only positive values (because F-statistics are the ratio of positive values). The p-value here is \(\Pr(F_0 > F)\), where \(F_0\) is the possible F-statistics under the null hypothesis. Let’s estimate this probability using pf():

# pf() estimate the probability of less than q
# Pr(F0 > F) is 1 - Pr(F0 < F)
p_value <- 1 - pf(q = f_value, df1 = n_g - 1, df2 = nrow(df_anova) - n_g)
print(p_value)

## [1] 0.00596054

5.3 ANOVA in R

Like the t-test, R provides functions to perform ANOVA easily. In this case, we will utilize the aov() function. The first argument of this function is the “formula,” which is used to describe the structure of the model. In our scenario, we aim to explain the fish body length by grouping them according to lakes. In the formula expression, we represent this relationship as length ~ lake, using the tilde symbol (~) to indicate the stochastic nature of the relationship.

# first argument is formula
# second argument is data frame for reference
# do not forget specify data = XXX! aov() refer to columns in the data frame
m <- aov(formula = length ~ lake,
         data = df_anova)

print(m)

## Call:
##    aov(formula = length ~ lake, data = df_anova)
## 
## Terms:
##                      lake Residuals
## Sum of Squares   105.9365 1467.6454
## Deg. of Freedom         2       147
## 
## Residual standard error: 3.159744
## Estimated effects may be unbalanced

The function returns Sum of Squares and Deg. of Freedom – these value matches what we have calculated. To get deeper insights, wrap the object with summary():

summary(m)

##              Df Sum Sq Mean Sq F value  Pr(>F)   
## lake          2  105.9   52.97   5.305 0.00596 **
## Residuals   147 1467.6    9.98                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The F-statistic and p-value are identical to our manual estimate.

5.4 Post-hoc Tests

When conducting an ANOVA and finding a significant difference among group means, a post-hoc test is often performed to determine which specific groups differ significantly from each other. Post-hoc tests help to identify pairwise comparisons that contribute to the observed overall difference.

There are several post-hoc tests available for ANOVA, including:

Tukey’s Honestly Significant Difference (HSD): This test compares all possible pairs of group means and provides adjusted p-values to control for the family-wise error rate. It is a commonly used and reliable post-hoc test.
Bonferroni correction: This method adjusts the significance level for each individual comparison to control the overall Type I error rate. The adjusted p-value is obtained by dividing the desired significance level (e.g., 0.05) by the number of comparisons.
Scheffe’s test: This test controls the family-wise error rate by considering all possible pairwise comparisons. It is more conservative than Tukey’s HSD, but it is suitable for cases where specific comparisons are of particular interest.
Dunnett’s test: This test is useful when comparing multiple groups against a control group. It controls the overall error rate by conducting multiple t-tests between the control group and each of the other groups.

The choice of post-hoc test depends on the specific research question, assumptions, and desired control of the Type I error rate. It is important to select an appropriate test and interpret the results accordingly to draw valid conclusions about group differences in an ANOVA analysis.

5.5 Laboratory

5.5.1 Application to `PlantGrowth`

In R, there is a built-in data set called PrantGrowth. To analyze this data set, carry out the following tasks:

The data set consists of two columns: weight, group. Create figures similar to Figure 5.1.
Conduct an ANOVA to examine whether there are differences in weight among the different group.
Discuss what values to be reported in a scientific article?

4 Two-Group Comparison

6 Regression